How to fit in: The learning principles of cell differentiation
by Miguel Brun-Usan
27 April 2020
The logic underlying cell differentiation has motivated an intense field of debate over years. How can plastic, developing cells “know” exactly where and how to differentiate ? Given that cells are aquipped with genetic networks, could they benefit from some form of basic learning, as cognitive systems do with neural networks? In our recent paper, we show that this idea goes beyond a simple metaphor: differentiating cells can exhibit basic learning capabilities that enable them to acquire the right cell fate. Although this statement could sound odd to some, we show how such a learning ability naturally arises from the way in which plastic cells integrate different signals from their environment during development. But to better grasp this connection, we have first to say a few words about the phenotypic plasticity of cells.
Phenotypic plasticity (i.e. the sensitivity of an organisms to its environment) is pervasive at every level of the biological hierarchy. For example, whilst part of the leaf morphology in plants is specific of each species, a great amount of variation in leaf size and shape can be linked to specific variations in the light, moisture and temperature conditions of the local environment. For those familiar with the topic, it is common to conceptualize plasticity as a “reaction norm”: an abstract function that link a specific environmental input to a phenotypic state. These reaction norms are often assumed to be genetically encoded and simple (e.g. linear) functions of a single environmental cue, so that phenotypes vary gradually in response to changes in one environmental variable (Fig. 1A).
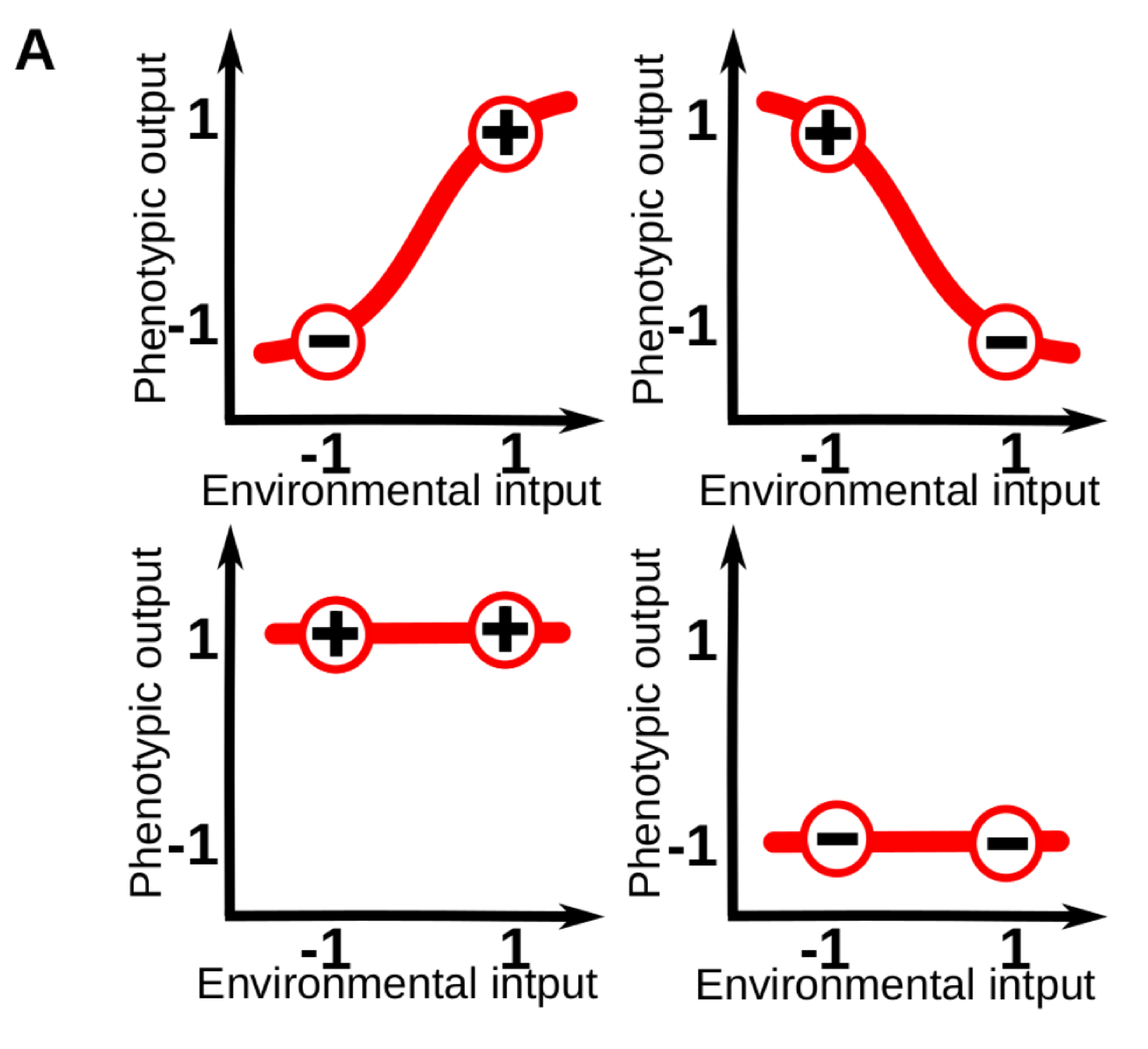
Figure 1A. Models of phenotypic and cell plasticity often depict a 1-dimensional reaction norm (red line), for a single continuous environmental cue.
Classic reaction norms are often a good approximation, but in reality the phenotypes are commonly determined by many environmental cues acting simultaneously. This is very relevant in the case of cell differentiation in multicellular organisms, where developing cells acquire their final fate by integrating several informational inputs from their surrounding tissue micro-environment (Fig. 1B).
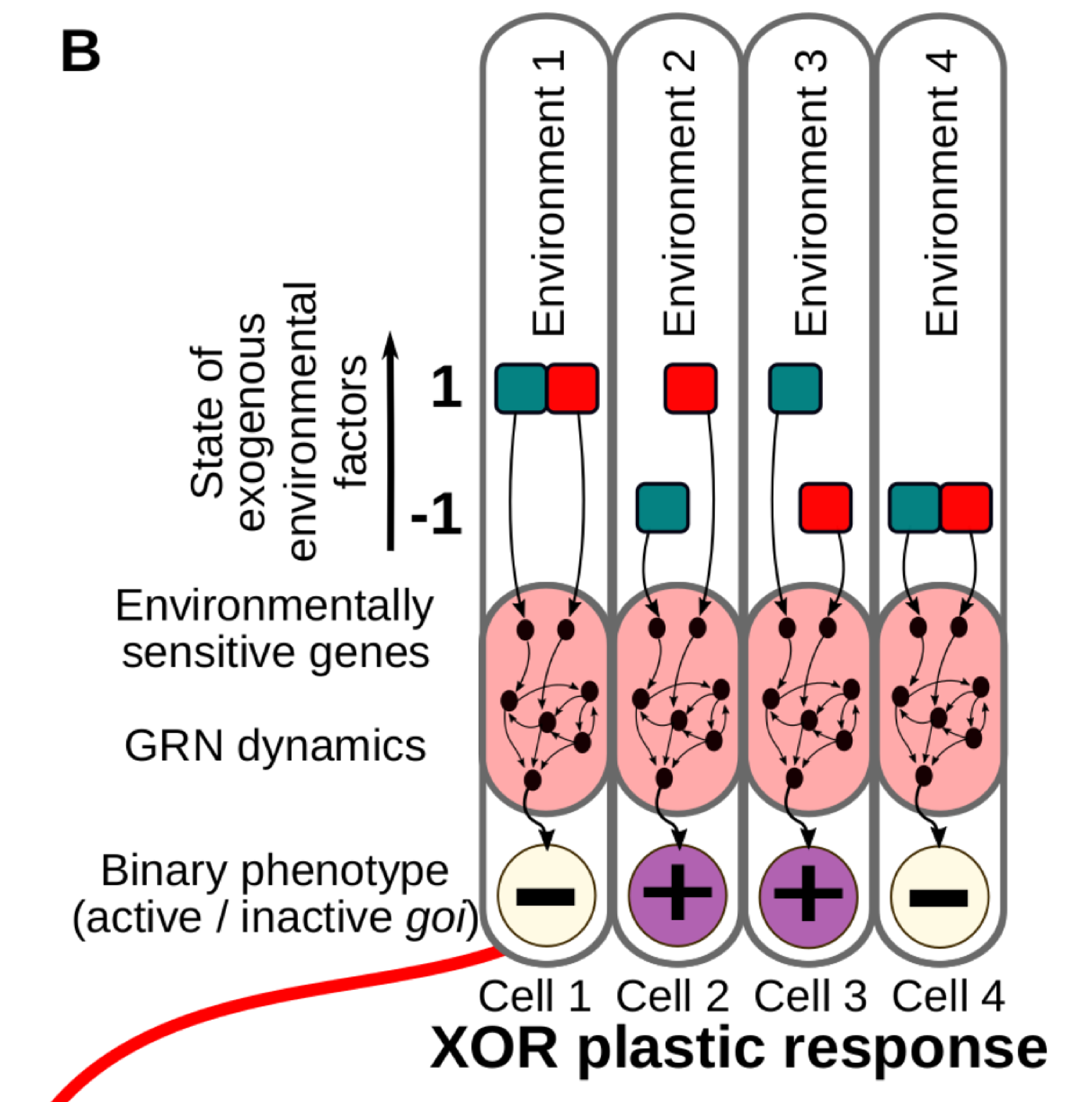
Figure 1B. We consider different combinations of Ne discrete environmental factors (in this illustrative example, Ne = 2, red and blue in the figure) determining a binary cell state. In this case, a number of possible environment-phenotype interactions can be described by means of logical functions derived from Boolean algebra (right).
These inputs include signalling molecules secreted by other cells, nutrients and chemicals taken up from the external environment, and even interactions between the embryo and other organism, such as the bacteria colonizing its skin and gut. Furthermore, the relationship between the environmental cues and the phenotypic responses can be highly non-linear. This calls for representations of plasticity in terms of “multi-dimensional” reaction norms, but these remain largely unexplored.
This work provides new conceptual tools to characterise these “multi-dimensional” reaction norms and to better understand how they arise and evolve, especially in the context of cell differentiation. In a nutshell, the relationship between the environmental cues (inputs) and cell phenotype (output) is described using Boolean logical functions (Fig. 1C).
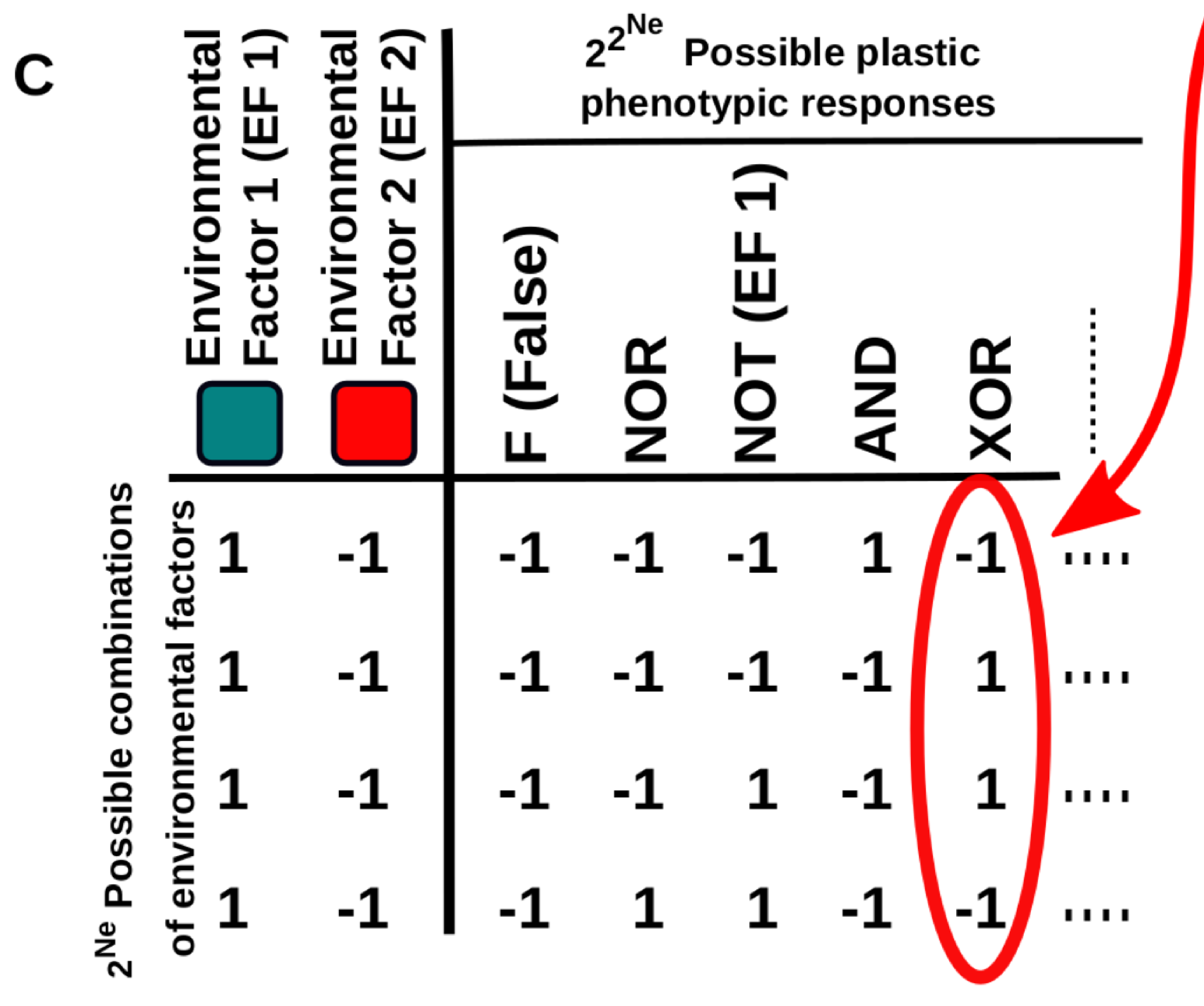
Figure 1C. Five examples of multi-dimensional reaction norms in which the expression level of some gene is affected by the Ne environmental factors. One of these multi-dimensional reaction norms (e.g. the one described by the “XOR” logical function depicted in B) is set as a target of a continuous GRN-based model.
This representation is very useful because it naturally introduces a way to measure the complexity of a multidimensional reaction norm: it will be very simple if the cell state is determined by one of the inputs, a little bit more complex if it is determined by a linear combination of the inputs (e.g. cell gets the state “A” if both inputs are negative and “B” otherwise) and maximally complex if the cell state is determined by a non-linearly decomposable function of the inputs (e.g. cell gets the state “A” if both inputs are equal -positive or negative- and “B” if they are different). In addition, this abstraction allows us to apply principles derived from computer science and learning theory to the study of cell plasticity.
By using a biologically realistic model of gene regulatory networks (GRNs), we show that natural selection is capable of discovering many forms of cell plasticity, even those associated with complex logical functions (Fig. 2B).
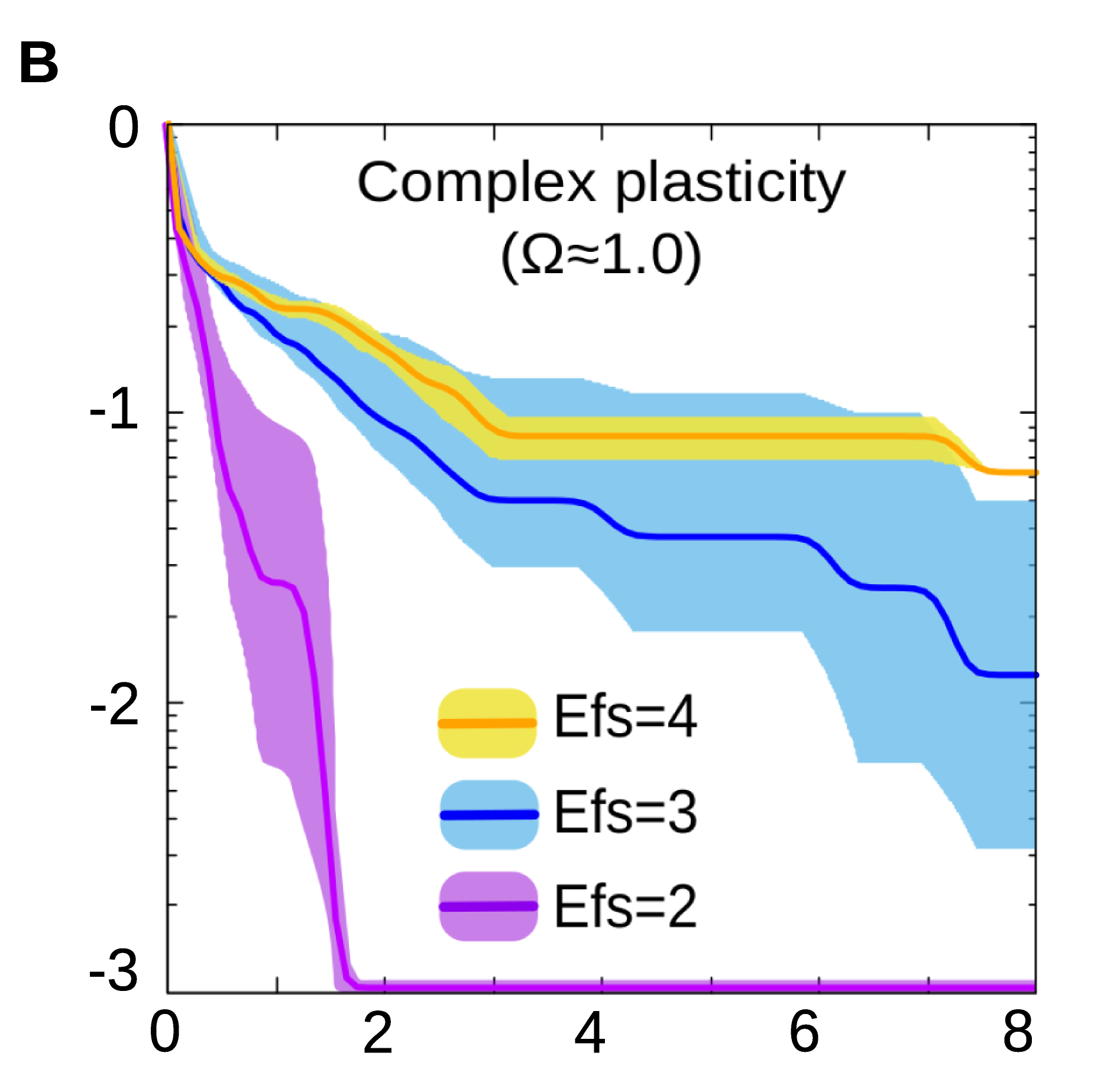
Figure 2B. In general, evolving a specific form of cell plasticity is faster when the number of environmental factors involved is low.
These later would correspond to scenarios where the cell state depends on the simultaneous integration of several environmental signals, but none of these signals alone contains enough information to determine the response (e.g. a response which is triggered if all the inputs are equal will require to know the state of every input, from the first to the last one).
This capability of plastic cells to evolve complex reaction norms is even more patent when the environmental signals modify the strength of regulatory interactions between genes. To illustrate this, take the phenotypic effect of temperature. Temperature does not to directly enhance or repress the expression of a gene but affects the kinetics of interactions between different gene products (Fig. 3A-B).
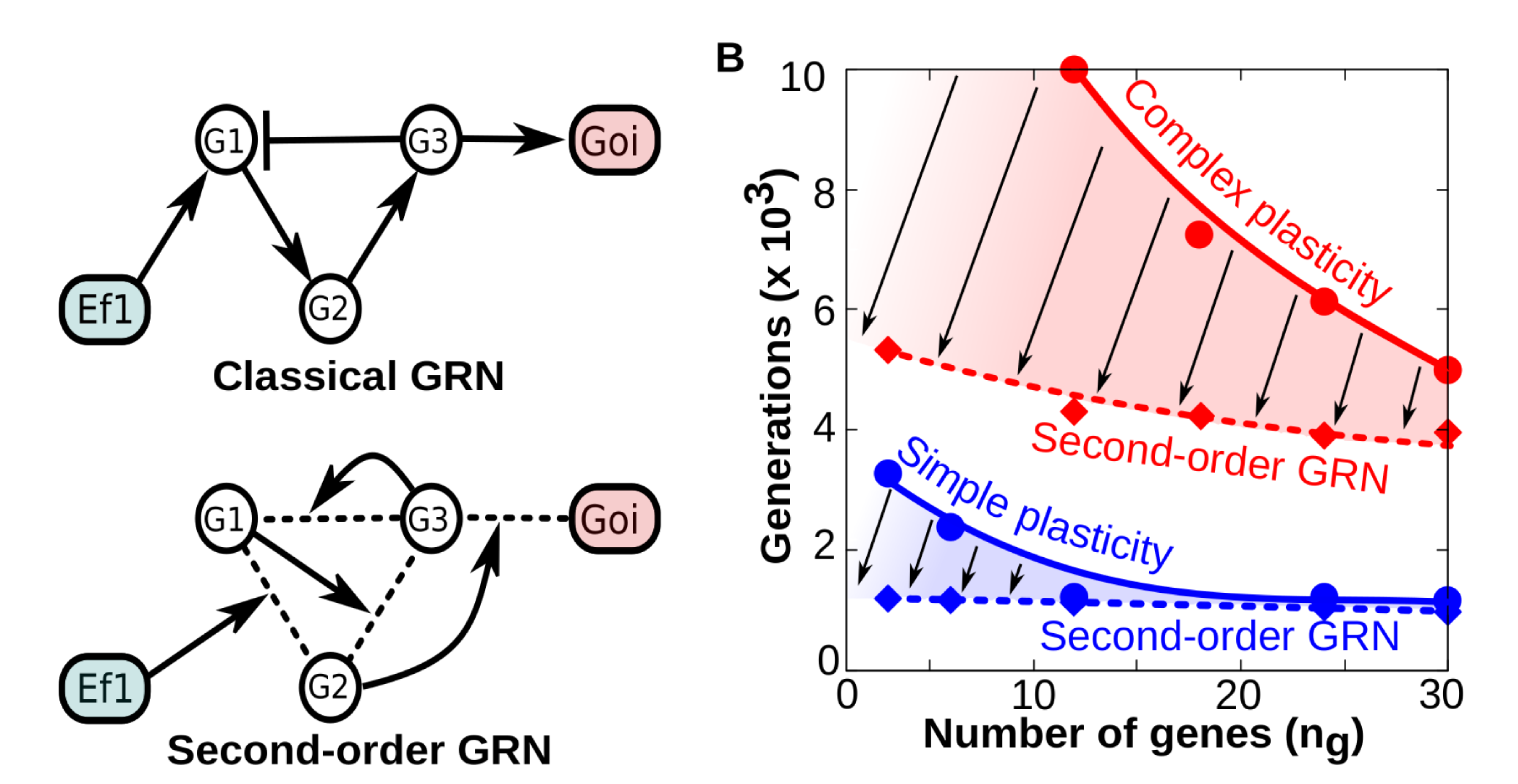
Figure 3A-B. A) Contrary to “classical” GRNs in which the network topology remains fixed over developmental time, second -order (tensor-based) GRNs have dynamical topology: each gene-gene interaction strength is determined by the concentration of other genes (g1, g2, etc) and environmental factors. In both cases the final phenotype is recorded as the binary state of a gene of interest (goi). B) Comparison between “classical” and “second-order” GRNs in terms of their evolvability (how many generations they need to achieve a fitness W≥0.95 when they are selected to represent specific reaction norms). The panel shows that everything else being equal (number of genes, function complexity), GRNs with dynamical topologies (dashed smoothed lines) require much less generations to evolve any reaction norm than classical GRNs (solid smoothed lines). Thus, GRNs capable of second-order dynamics exhibit higher evolvability than classic GRNs (being the difference more patent for complex forms of plasticity).
Simulations also reveal that developmental dynamics produces a strong and previously unnoticed bias towards the acquisition of simple forms of cell plasticity. This bias causes linear reaction norms to be far more likely to appear than humped-shaped or sigmoidal ones, and appears even in random (i.e. not evolved) GRNs. This suggests that this bias towards simple plastic responses is an inherent feature GRN dynamics rather than a derived property (Fig. 4A).
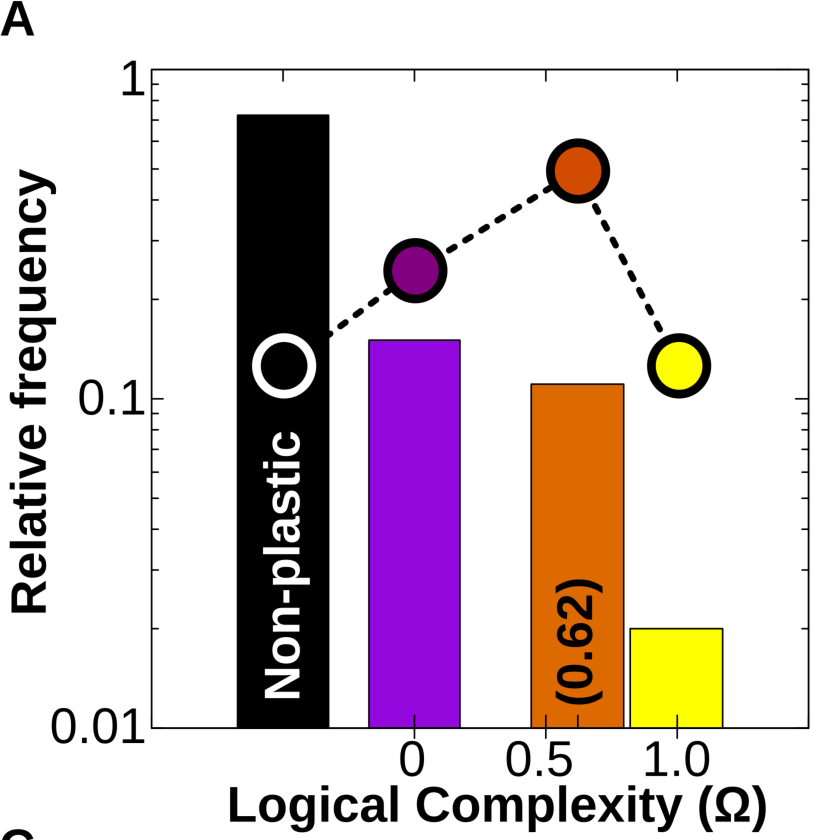
Figure 4A. (Log) Relative frequency of different types of cell plasticity according to their complexity Ω in a vast GRN space. Black column: no plasticity (the phenotypic state is purely determined by genes); purple column: phenotypic state directly determined by just one of the Ne environmental factors; orange column: phenotypic state determined by simple combinations of the Ne environmental factors (linearly decomposable functions) and yellow column: complex forms of cell plasticity associated with non-linearly decomposable functions (XOR, XNOR; see SI). Dashed line and dots represent the relative distribution of each family of logical functions in the mathematical space. We see that although the number of simple and complex functions that exist is approximately equal, GRNs produce simple functions much more often.
In a second set of experiments, we explored the evolutionary consequences of that bias. These experiments show that, when the selective environment mirrors the plastic bias of development (that is, when simple reaction norms have higher adaptive value), plastic cells are able to display appropriate plastic responses even in environmental conditions that they have never experienced. This ability to generate variation is a form of basic learning. New variation is not produced at random, but in an advantageous direction (Fig. 6A-B).
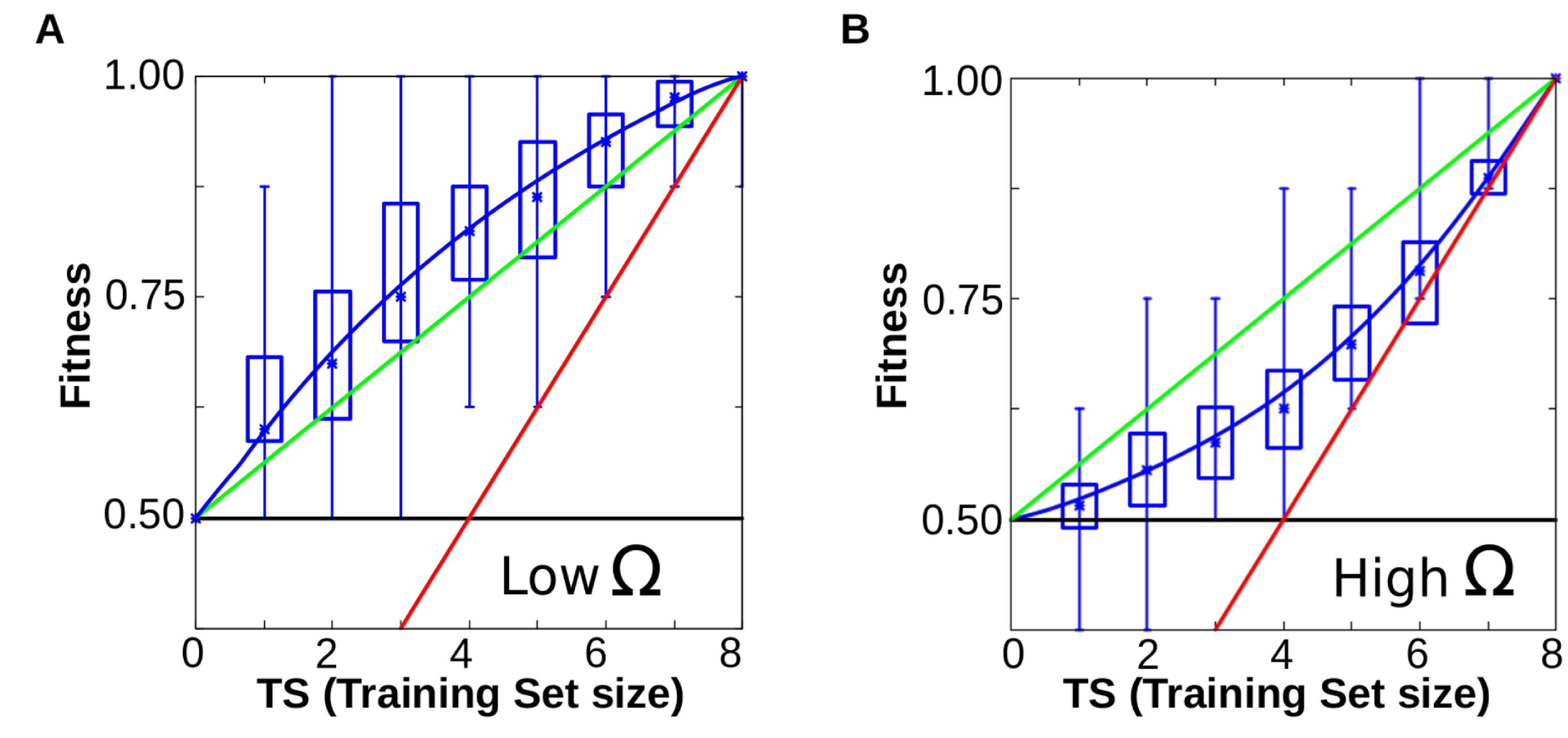
Figure 6A-B. When cells evolve simple forms of plasticity, they are able to generalise, performing better than chance in previously unseen environments (red line represents the information provided (x = y), green line represents the expected performance at random (2Ne-TS)/2; and blue line the degree of matching between the resulting phenotypes and the expected ones for a given function). Notice that blue line runs consistently higher than the green line (random response). B. Similar experiments yield poor performances when cells have to evolve complex forms of plasticity (blue line below the green one, see main text).
As a proof of principle, this work shows how differentiating cells can take advantage of such basic learning to acquire the right cell fate even in noisy developmental conditions (Fig. 7).
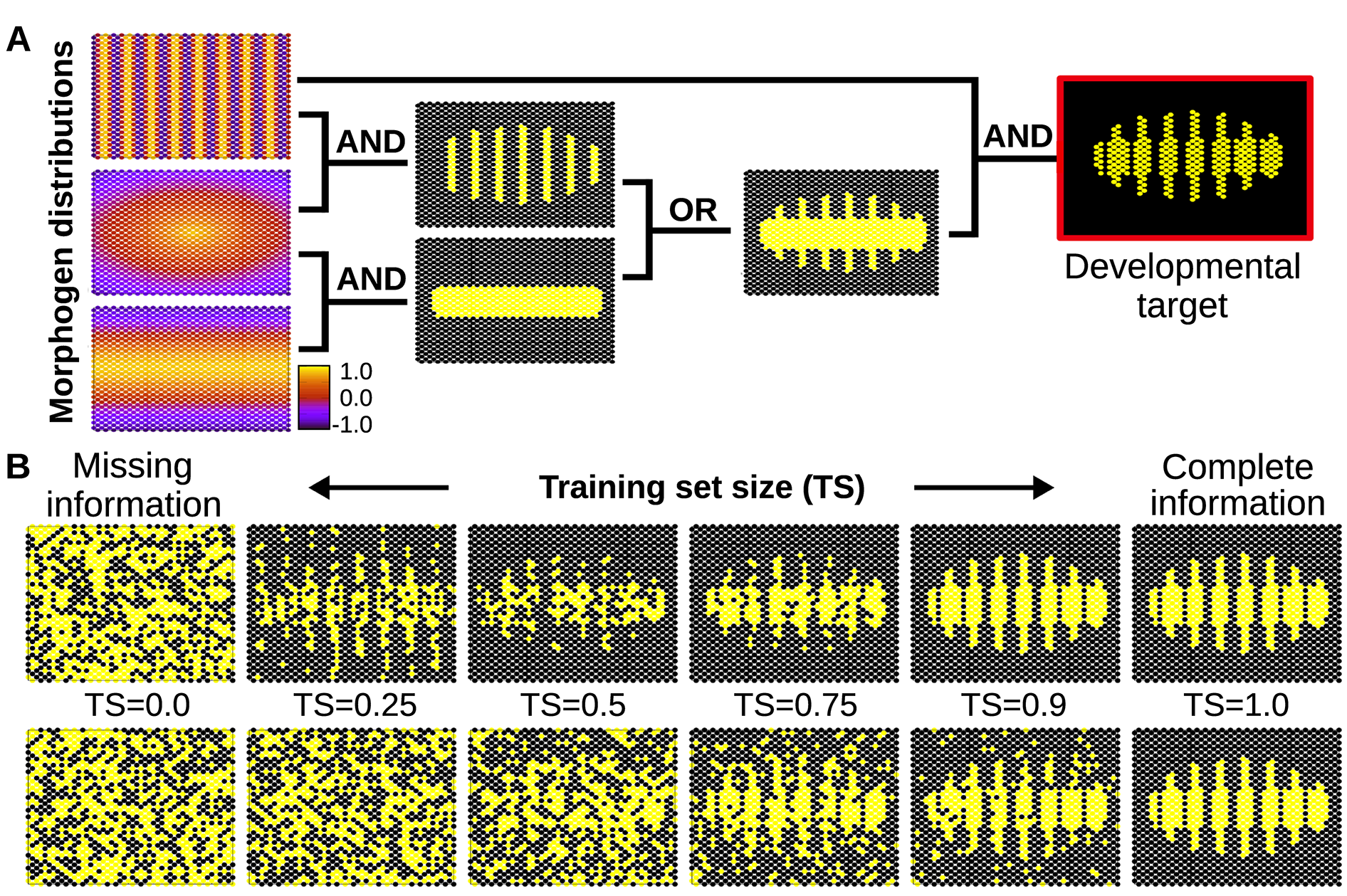
Figure 7. A) Simple spatial distribution of three morphogens over a two-dimensional (50×25) field of cells (similar gradients are commonly found in the early developmental stages of many organisms). In this example, these three environmental signals are integrated by individual cells (according to relatively simple logical functions) to form a segmented developmental pattern. The complete plasticity function is represented by a truth table of 32 rows specifying whether the relevant cellular output should be on or off for each possible combination of morphogens (see Methods). B) Individual cells are evolved under selective conditions that expose them to some rows of this table but not all. Under this scenario of missing selective information, cells equipped with real GRNs perform by default a simple logical integration of the morphogen cues, which in this example results in a much more robust and uncertainty-proof developmental process (upper row). When the training set contains all the information necessary to completely define the plasticity function, natural selection finds a GRN that calculates this function accurately (right). Of course, when past selection contains no useful information, the phenotype of the GRN is random (left). In between we can see that the generalisation capability of the evolved GRN ‘gives back more than selection puts in’- i.e. the phenotype produced (top row middle) is visibly more accurate than the training data experienced in past selection (bottom row middle). This is quantified in S1 Fig. In the bottom row, cells do not exhibit any bias towards simple functions, and therefore they acquire any random form of plasticity compatible with the previously experienced environmental inputs. This randomness in the plastic response fails to fit the required (target) function, preventing generalisation (i.e. the system needs to evolve in a full-information scenario to produce the required phenotype, see main text).
If the developmental pattern emerges from a simple integration of many signals, the cells do not need to receive every signal to trigger the appropriate response: they will unleash a complete and adequate response from just a few inputs. The cells will most likely provide the right answer because they do not consider the whole, vast space of possible responses, but just a few simple, adaptive solutions compatible with the few bits of environmental information received. Metaphorically, this could be seen as if plastic cells would able to apply a sort of Occam’s razor parsimony principle to the developmental problems they must solve. This finding identifies a novel mechanism that increases the robustness of developmental process against external perturbations.
Overall, this work illustrates how learning theory can illuminate the evolutionary causes and consequences of cell plasticity. This approach is possible because learning principles and logical rules are not substrate specific: they can be exhibited by interacting molecules, genes, cells, neurons and transistors alike as long as these elements have the right type of interactions. This substrate independence of learning principles helps interpret the main finding of this work: that evolving gene networks can exhibit adaptive principles similar to those already familiar in cognitive systems.
Read the original article here: Brun-Usan M, Thies C, Watson RA. 2020. How to fit in: The learning principles of cell differentiation. PLOS Computational Biology. 16(4):e1006811.