The philosophy of social evolution
by Jonathan Birch
1 November 2017

Fruiting bodies of the social amoeba Dictyostelium discoideum. Image: Usman Bashir
To coincide with the publication of his latest book, The Philosophy of Social Evolution, philosopher Jonathan Birch is this week’s guest blogger on The Brains Blog. Read his series of posts below.
Part 1. Altruism in nature
Part 2. Relatedness and altruism
Part 3. Relatedness, time and bacteria
Part 4. The social organism
Part 5. Cultural inclusive fitness?
Part 1. Altruism in nature
What is biological altruism? We tend to think of altruism as action motivated by concern for others. Biologists, however, use the term in a different way. In biology, altruism is, roughly speaking, behaviour that has two distinctive consequences for reproduction: it reduces the chances of reproduction of the organism that performs the behaviour, and it increases the chances of reproduction of another organism [1]. The easiest way to grasp this idea is through a few examples.
Insects
Ants, wasps and bees are everyone’s favourite biological altruists. In species known as “eusocial”, there is a division of labour between the workers and the queen: the workers sacrifice their own chances of reproduction to raise the queen’s larvae. Some ants become living ‘honeypots’, hanging upside down from the roof of the nest, storing food for the rest of the colony. An especially poignant example of self-sacrifice is found in a species of Brazilian ant, Forelius pusillus. At the end of each day, some of the workers will seal the entrance to the nest from the outside, protecting it from nocturnal predators—but dooming themselves to die in the cold night-time temperatures.
One might object: is this really biological altruism, if the workers are sterile? I said biological altruism reduces an organism’s chances of reproducing—but doesn’t a sterile worker ant have zero chance of reproduction no matter what it does? In fact, only in a few species of ant are the workers fully sterile. In most species, workers can produce eggs which (though unfertilized) can develop into males—but the vast majority never activate their ovaries. In those species in which the workers are fully sterile, they are still biological altruists, but we should think about their altruism in a different way. We should say that these ants’ entire developmental process, rather than any specific behaviour, is altruistic. The whole process of developing into a sterile worker confers benefits on others at a cost to self.
Microbes
Some of the most spectacular acts of self-sacrifice in nature are too small for the naked eye to see. Consider the social amoeba Dictyostelium discoideum. For much of their life cycle, these amoebae live as single-celled organisms. But when food gets scarce, the amoebas start signalling to their neighbours. If they find out that other amoebas are present in sufficient numbers, the starving amoebas aggregate to form a mobile slug called a ‘pseudoplasmodium’ or ‘grex’. The grex moves as one, further and faster than any individual amoeba could, in the direction of heat and light. On reaching a favourable location, the slug stops and begins to transform into a fruiting body.
Around a fifth of the amoebas sacrifice their lives in this process, forming a hardy, cellulose stalk of dead cells. The remaining four fifths cluster at the tip of the stalk, where they generate and release spores. The spores are dispersed through the environment, reducing the chances that the amoebas they ultimately produce will encounter the same harsh conditions their parents endured.
It turns out that cooperation, albeit usually less dramatic than this, is pervasive in microbial populations. We now realize that what looked like a blob on a Petri dish is in reality a dynamic social network: a community in which vast numbers of microorganisms, often including members of several different species, interact with each other in complex ways. Perhaps the most frequent type of cooperative interaction involves the production and consumption of so-called ‘public goods’. These goods include enzymes, surfactants, antibiotics, adhesive polymers, ammonia, and other useful molecules. What they have in common is that, when emitted by a producer into the external environment, they confer a benefit on at least some other nearby microorganisms.
Humans
Humans, in their best moments, are capable of matching the heroism of ants and amoebas. Tales of ant-like self-sacrifice are the stuff of legend in many cultures. When the pioneering evolutionary theorist John Maynard Smith wanted a historical example to add colour to his model of the evolution of signalling, he reached for the tale of Philip Sidney, an Elizabethan aristocrat mortally wounded at the Battle of Zuphen. The legend goes that, as he lay dying, he handed his water to another wounded soldier, remarking ‘thy necessity is yet greater than mine’. He did not turn his abdomen into a living water tank and spend his life hanging from the ceiling, drip-feeding others, but he still deserves some credit.
For many Britons, the iconic example of self-sacrifice is that of Captain Oates, a member of the ill-fated British Antarctica Expedition of 1910-13. Suffering from gangrene and frostbite, and seeing that he was impairing the survival chances of the rest of the expedition, he left the tent and walked into a blizzard, remarking ‘I am just going outside and may be some time’. Ants of the species Temnothorax unifasciatus do something similar. When infected by a fungal pathogen, they leave the nest to die alone, minimising the risk of transmission of the disease to nestmates.
Prosocial behaviour
Such acts are the exception rather than the rule in human social life. But while extreme self-sacrifice may be unusual, an everyday, low-key form of ‘prosocial’ behaviour is the glue that holds human societies together. Just as an ant colony relies on countless workers unspectacularly bringing food to the nest, and a bacterial biofilm relies on the sharing of molecular ‘public goods’, human societies are held together by the fact that we are not all free riders. We help each other. We do public-spirited things like paying taxes, doing voluntary work, and voting in elections.
In modern societies, just as in some ant colonies, some of these behaviours are coerced: we’d be punished if we didn’t do them. Moreover, we have reputations to maintain, and sometimes our reputation would suffer if we didn’t do these things. But this is not true in all cases, and it is not a sufficient explanation for human social behaviour. There is a general human tendency towards prosociality that can still be seen in most people even when coercion and reputational benefit is stripped away. We see it in such real-world phenomena as anonymous charity donations and donations of blood and tissue, as well as in simple economic experiments.
Extreme heroism aside, is public-spirited behaviour biologically altruistic? Does it really detract from your chances of reproducing? Sometimes it does: organ donations by living donors are an obvious example. It’s less obvious that taking a financial hit, as in the case of a charity donation, is biologically altruistic. In some cases, it may even increase your chances of reproducing by improving your attractiveness to potential sexual partners. Whether or not a behaviour is biologically altruistic depends on its long-term effect on an organism’s chances of reproduction over the course of its entire lifetime, and that can be hard to assess. This is why the term ‘prosocial’ is helpful. Many everyday human behaviours are clearly ‘prosocial’ in a broad sense, whether or not they are biologically altruistic.
The search for common principles
Are there common principles powerful enough to help explain biological altruism and prosocial behaviour wherever we find it in the natural world—in amoebas, ants, humans and beyond? My book The Philosophy of Social Evolution explores this question. My answer, in short, is that relatedness is the crucial unifying concept, and W. D. Hamilton’s theory of inclusive fitness tells us how to use relatedness to make sense of social behaviour. Inclusive fitness is a familiar idea for many biologists—less so for philosophers—but the application of this idea to microbial evolution and cultural evolution introduces new challenges.
In this series of blog posts, I’ll introduce some of the main ideas from the book [2]. In Part 2, I’ll present the basic idea of inclusive fitness and explain why it matters. In Part 3, I’ll consider some of the complications that arise when applying inclusive fitness to evolution in microbes. In Part 4, I’ll discuss the idea that a multi-celled organism is itself a form of social group—a social group of cells, or ‘cell state’—and ask whether social evolution theory can help make sense of why multicellular organisms exist. In Part 5, I’ll turn to humans, and argue that inclusive fitness has a useful role to play in theories of cultural evolution.
[1] I say ‘roughly speaking’ because there are some ways in which I think we should revise and refine this definition (see Chapter 1 of The Philosophy of Social Evolution), but I won’t go into those details here.
[2] These blog posts will introduce the ideas in a non-technical way. Readers looking for a more detailed introduction to some of the ideas in the book may want to take a look at Jonathan Birch, 2017, ‘The Inclusive Fitness Controversy: Finding a Way Forward’, Royal Society Open Science 4:170335.
This post was originally published on The Brains Blog, 30 October 2017
Part 2. Relatedness and altruism

Image: Jonathan Birch
Haldane’s quip
In what circumstances might natural selection favour self-sacrifice? As legend has it, the best known answer to this question was first spoken in a London pub called the Orange Tree. One night in the 1950s, after “calculating on the back of an envelope for some minutes”, J.B.S. Haldane remarked to John Maynard Smith—at the time, one of his graduate students—that “he was prepared to lay down his life for eight cousins or two brothers”.
If the story is true (and Maynard Smith insisted it was, though this has been disputed over the years), Haldane had latched on to a deep insight about the evolution of altruism. He had seen that genetic relatives have an evolutionary incentive to help one another. He had also seen that the incentive comes in degrees, and that the size of the incentive depends on the closeness of the helper’s genetic relationship to the beneficiary.
Haldane may not have been the first to see these things (R. A. Fisher grasped the basic point two decades earlier), but he may have been the first to glimpse their potential explanatory power. In a 1955 article [1], he illustrated these ideas with a vivid example:
‘Let us suppose that you carry a rare gene which affects your behaviour so that you jump into a river and save a child, but you have one chance in ten of being drowned, while I do not possess the gene, and stand on the bank and watch the child drown. If the child is your own child or your brother or sister, there is an even chance that the child will also have the gene, so five such genes will be saved in children for one lost in an adult. If you save a grandchild or nephew the advantage is only two and a half to one. If you only save a first cousin, the effect is very slight. If you try to save your first cousin once removed the population is more likely to lose this valuable gene than to gain it.’
He went on, however, to suggest that this idea was probably more applicable to insects than to humans:
‘But on the two occasions when I have pulled possibly drowning people out of the water (at an infinitesimal risk to myself) I had no time to make such calculations. Palaeolithic men did not make them. It is clear that genes making for conduct of this kind would only have a chance of spreading in rather small populations where most of the children were fairly near relatives of the man who risked his life. It is not easy to see how, except in small populations, such genes could have been established. Of course the conditions are even better in a community such as a beehive or an ants’ nest, whose members are all literally brothers and sisters.’
Although Haldane never captured these thoughts in a detailed model, we can see here the subtlety of his thinking. He saw a gene for altruism might spread if the benefits fell differentially on other bearers of the gene, but he also saw that a mechanism that relied on organisms consciously calculating degrees of kinship was implausible. His proposed solution was small populations or communities: if a population or community is so small that everyone is a close relative of everyone else, the benefits of altruism will tend to fall on genetically similar individuals without the need for conscious calculation.
Hamilton’s rule
The Orange Tree was demolished in the spring of 1963. In the aftermath of the demolition, the Beatles arrived for a photoshoot, and a shot of them leaping above the rubble of Haldane’s old haunt would be used as the cover for their 1963 EP, Twist and Shout. Elsewhere in London, a graduate student called Bill Hamilton was making leaps of his own on Haldane’s foundations. He was working on a manuscript called ‘The Genetical Evolution of Social Behaviour’—a manuscript that would change the way we think about the evolution of altruism [2].
Hamilton had arrived at a more general form of Haldane’s insight, and he had captured it in a detailed mathematical framework. Crucially, he showed that the general sort of process Haldane had described did not require ‘rare genes’ or ‘rather small populations’. Fundamentally, what is required is that the benefits of altruistic behaviour fall on recipients more likely than average to possess the genes for altruism.
Hamilton realised that the evolution of altruism depends, in a surprisingly simple way, on the cost to the actor and the benefit to the recipient—measured in the currency of reproductive success, or expected number of offspring—and on the closeness of the genetic relationship between them. In short: if sufficiently large benefits fall on sufficiently related recipients to offset the cost to the altruist, altruism can evolve by natural selection.
The precise mathematical relationship between cost, benefit and relatedness is captured in a principle now known as Hamilton’s rule. The rule states that a social behaviour will be favoured by natural selection if and only if rb > c, where ‘b’ is the effect of the behaviour on the reproductive success of others, ‘c’ is the effect on one’s own reproductive success, and ‘r’ is the coefficient of relatedness, which measures the statistical association between the genes of the actor who performs the behaviour and the genes of the recipient affected by it.
The easiest way to understand the rationale behind the rule is to take a ‘gene’s eye’ perspective. Imagine that you are a gene—what matters to you is the number of copies of yourself you leave in future generations. You have two ways to achieve this goal: a direct way and an indirect way. The direct way is to promote the reproductive success of the organism in which you are located. The indirect way is to promote the reproductive success of other organisms—provided those organisms are sufficiently likely to transmit copies of you to their offspring to make them worth the investment. Suppose a chance to help another organism arises. Should you help that organism or not? Hamilton’s rule can be thought of as capturing the cost-benefit calculation you have to make.
Having said that, I immediately want to row some of it back. The gene’s eye view makes Hamilton’s ideas easier to understand—as Richard Dawkins, one of Hamilton’s great champions over the years, is well aware. But gene’s eye thinking and inclusive fitness theory are not the same. Inclusive fitness theory involves taking an organism-level perspective, and estimating costs and benefits at the level of the organism. The goal is to explain the evolution of an organism-level trait (social behaviour) in terms of properties of interactions between organisms (costs, benefits and coefficients of relatedness) while recognising that these properties depend on the organisms’ genetic makeup. Thus inclusive fitness theory is, and always has been, an interesting hybrid of gene-level and organism-level thinking, and a proper interpretation of the theory needs to do justice to both its gene-centred and organism-centred aspects.
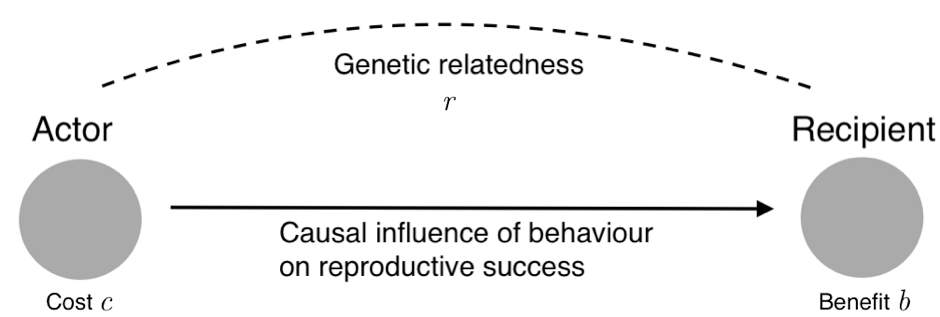
Hamilton’s rule: the genes for a social behaviour are selected if and only if rb > c, where b is the benefit conferred on a recipient, c is the cost imposed on the actor, and r is the coefficient of relatedness. (Figure from J. Birch, 2017, The Philosophy of Social Evolution, Oxford: Oxford University Press, © The Author.)
The rule under attack
Your initial reaction to Hamilton’s rule might well be: how can it be so simple? Aren’t the dynamics of natural selection messy and complicated? How can such a simple rule be anything more than an approximate rule of thumb, or perhaps a result that holds in certain special cases, given restrictive assumptions, but not in others? This is also the reaction of many mathematically trained biologists, and has been ever since Hamilton first derived the rule. A 2010 Nature article by Martin Nowak, Corina Tarnita and Edward O. Wilson kicked off a new round of debate on this issue—one that is still on-going.
Two chapters of The Philosophy of Social Evolution are devoted to this issue—far too little space to do justice to all of the objections thrown at Hamilton’s rule over the course of half a century. After studying this literature for some time, I’m fairly convinced that there is a version of Hamilton’s rule that is simple, exact, mathematically correct and surprisingly general. This is the version derived by David Queller in his 1992 paper ‘A General Model for Kin Selection’.
In this version, the famous ‘rb > c’ form is still there, but the cost, benefit and relatedness coefficients have somewhat counterintuitive meanings. They are population statistics, calculated by averaging over all interacting pairs of organisms—not properties of ‘token’ social interactions. These population statistics abstract away from messy detail to capture the overall statistical associations in a population between an organism’s genes, its own reproductive success, the genes of its social partners, and its social partners’ reproductive success.
People hear ‘cost’ and ‘benefit’ and think ‘payoffs’—but, except in very simple cases, cost and benefit are not payoff parameters but complicated functions of payoff parameters. Likewise, people hear ‘relatedness’ and think ‘family trees’—but, except in very simple cases, relatedness cannot simply be read off from a family tree. It depends in complicated ways on the structure of the population. In short, r, b and c can depend in all kinds of ways on the population structure and the payoffs of social interaction, depending on the details of the case.
The precise way in which r, b and c depend on these parameters has consequences for how they change over time—and for what evolves over the long run. If rb > c now, the trait is being selected now—but what happens next depends on how r, b, c change as the population changes, and this can be very complicated indeed. Queller’s version of Hamilton’s rule thus provides a momentary snapshot, at a high level of abstraction, of underlying dynamics that are in fact every bit as messy and complicated as you would intuitively expect.
The organizing role of Hamilton’s rule
What’s the use of an abstract, high-level, statistical snapshot of a complex dynamical process? For some critics, this is a rhetorical question—the rule is simply useless. I disagree. I think snapshot principles of this type (other examples of which, by the way, include Price’s equation and Fisher’s ‘fundamental theorem’) are very useful for organizing our thinking about evolution. They are organizing frameworks, and Hamilton’s rule provides an organizing framework for the study of social evolution. It is no substitute for detailed modelling of evolutionary processes—but it is not intended to be. What it does is provide a framework in which we can tease out the common features of an apparently diverse class of models.
In particular, the rule tells us that any model in which true biological altruism (i.e. behaviour that detracts from the lifetime reproductive success of the actor and increases that of the recipient) evolves by natural selection must contain at least one source of positive ‘relatedness’, construed very broadly—that is, it must contain at least one source of positive genetic assortment between social partners. If you think you’ve made a model in which altruism evolves without positive genetic assortment, one of three things is going on:
(i) the model implicitly contains a source of positive genetic assortment;
(ii) the behaviour is not altruistic in the sense of imposing a long-term cost on the actor (perhaps a short-term cost is offset by long-term gain, as in cases of ‘reciprocal altruism’);
(iii) an evolutionary process other than natural selection is driving the evolution of the trait.
What is ruled out by Hamilton’s rule is the evolution of altruism by natural selection without any positive genetic assortment at all. I know of no empirical examples that should lead us to rethink this result. What we find in amoebas, ants, bees, wasps, baboons, wolves, and all kinds of other species is that the benefits of altruism are indeed directed differentially towards genetically related recipients. Humans are an interesting case, often proposed to be an exception—we’ll consider them in Part 5.
As Hamilton emphasized, there are many possible sources of positive genetic assortment, including kin recognition, group-mate recognition, shared habitat preference, limited dispersal from the group, and more. What Hamilton’s rule allows us to see is that all such mechanisms enable the evolution of altruism for fundamentally the same reason—they all cause the benefits of altruism to be directed towards other bearers of the genes for altruism, making it possible that, in the right circumstances, rb might outweigh c.
In Part 3, I introduce an unusual, fascinating but poorly understood source of positive genetic assortment that arises in the world of microorganisms. That mechanism is horizontal gene transfer.
[1] J. B. S. Haldane, 1955, ‘Population Genetics’, in Johnson, Abercrombie and Fogg, eds, New Biology 18. London: Penguin, p. 44.
[2] W. D. Hamilton, 1964, ‘The Genetical Evolution of Social Behaviour’ I and II, Journal of Theoretical Biology, 7:1-52.
This post was originally posted on The Brains Blog, 31 October 2017
Part 3. Relatedness, time and bacteria

Fruiting bodies of the myxobacteria, as sketched in 1892 by Roland Thaxter (compiled by the English Wikipedia).
In Part 1, we saw that cooperative behaviour is rife in the world of microorganisms. The fruiting bodies of myxobacteria and social amoebas are famous, but any bacterial biofilm is held together by vast amounts of discreet cooperation—the bacteria emit all kinds of molecular ‘public goods’ to their neighbours.
This cooperative behaviour isn’t always altruistic, in the sense of implying a life-long cost to the reproductive prospects of the producer. It is often hard to tell whether the production of a public good is altruistic or not. But since these public goods are often energetically costly to produce, their production may well be altruistic in at least some cases.
So what stabilizes the production of these costly public goods against the threat of free-riding? The basic answer is probably a familiar one: relatedness. Many of a bacterium’s immediate neighbours are members of the same strain, and as such are clonally related to it. Although biofilms often contain multiple species, most of the cooperation happens within species—inter-species interactions are mostly competitive. So Hamilton’s ideas are as relevant here as they are to large, multicellular organisms.
Gene mobility
When we apply Hamilton’s ideas to bacteria, however, complications arise. The source of the trouble is the tendency of bacteria to exchange genes ‘horizontally’—for example, by transferring small packets of DNA called ‘plasmids’ through a process of cell-to-cell contact called ‘conjugation’. A growing body of evidence points to the importance of this process to social evolution in bacteria. It turns out that many of the genes implicated in producing public goods are actually carried on plasmids.
What is going on here? The key point is that plasmid transfer is a replicative process: the plasmid is copied from one cell to another. So, after conjugating, two nearby organisms may share genetic material they did not share before. We can therefore see how, at least in principle, plasmid transfer can lead to genetic similarity between organisms.
Plasmid transfer is thus a source of ‘relatedness’ in the broad sense that matters in social evolution theory. It’s a process that causes bearers of the genes for a social trait to cluster together, so that the effects of that trait fall differentially on other bearers of the relevant genes. Recently, experiments by Tatiana Dimitriu et al. have provided some experimental evidence that this really happens—plasmid transfer really does lead to higher relatedness, and really does allow a plasmid that encodes a public good to spread more rapidly than a plasmid that does not.
Why is that? Think about it this way: the altruism-encoding plasmid, by transferring horizontally, forcibly converts nearby free-riders into altruists. Because it targets nearby free-riders, not random free riders, it generates the sort of clustering together of altruists that allows altruism to become evolutionarily advantageous. When the public good is produced, the benefits fall differentially on other organisms who carry the genes for producing it.
This is easiest to imagine if we imagine the free-riders being forcibly converted into altruists early in the life-cycle—so that organisms who converted them have time to reap the benefits of having altruistic neighbours. But there’s also a more subtle (and harder to imagine) variant of the process in which the free-riders are converted late in the life-cycle.
In this variant, altruists first help their neighbours by producing a public good, and only later convert nearby free-riders, after they have already done their free-riding. This time, the benefits of altruism don’t fall differentially on current bearers of the genes for altruism, but they do fall differentially on potential future bearers of those genes—and that too might, in the right circumstances, be enough to make altruism evolutionarily advantageous.
Rethinking relatedness
This is already a rather subtle and difficult idea—but unfortunately the complications don’t end there. Gene mobility has foundational implications for social evolution theory. If we want a theory that fully incorporates the effects of horizontal gene transfer on relatedness, we need to change the way we think about relatedness. Here, in short, is why (see Chapter 6 of The Philosophy of Social Evolution for further detail).
In multicellular animals like humans or ants, relatedness can often be estimated fairly well by looking at genealogy—the extent to which interacting organisms have ancestors in common. This isn’t always the best way to measure relatedness, and in recent years genealogy-based measures have given way to statistical measures of genetic similarity estimated using molecular markers. But what is still taken for granted by all of these measures is that an organism’s genome remains stable over its life cycle, so that the time in the life cycle at which you measure relatedness doesn’t really matter—the same animal will always have the same genes.
When genes for social traits are being transferred horizontally, an organism’s genome is not stable over the course of its life-cycle, and the time at which you measure relatedness really does matter. In fact, what matters fundamentally is not whether the actor and recipient share genes at the time they interact, but whether the recipient is a potential future bearer of the actor’s genes—a potential candidate for transmitting those genes to future generations.
The easiest way to see this is to take a ‘plasmid’s eye view’ on the process. If you’re a gene carried on a plasmid, you value your own host as a route to future generations—but you also value potential future hosts. It might still be in your evolutionary interests to help a nearby organism that is not yet carrying a copy of you, if it might, in the future, conjugate with your host and acquire a copy. The best measure of ‘relatedness’ in this context is one that assigns value to potential future hosts not on the basis of their current genetic makeup, but on the basis of how likely they are to transmit a copy of you to their descendants.
This way of thinking about relatedness is fundamentally diachronic: relatedness is really about genetic similarity between one organism at the moment of gene expression and another organism at the moment of gene transmission, not about genetic similarity between two organisms at the same time. In other words, it is not a synchronic relation between two simultaneous ‘time-slices’ of organisms, but a diachronic relation between two temporally separated time-slices. That is an unfamiliar, non-intuitive way of thinking about relatedness—but it is one we may have to get used to as we learn more about social evolution in bacteria.
In short, we tend to think that whether or not two organisms count as ‘genetically related’ depends on their present (whether or not they share genes now) and on their past (whether or not they have parents or other ancestors in common). But what really matters in evolution is the future. To assess whether an altruistic behaviour will be favoured by selection, the fundamental question is not ‘Do the actor and recipient have recent ancestors in common?’ or even ‘Does the actor genetically resemble the recipient now?’ The question is: ‘Will this behaviour increase the representation in future populations of the genes it expresses?’ In microbes, the answer can be ‘no’ to the first two questions but ‘yes’ to the third.
This post was originally published on The Brains Blog, 1 November 2017
Part 4. The social organism

Fruiting bodies of the myxobacteria, as sketched in 1892 by Roland Thaxter (compiled by the English Wikipedia).
The ‘cell state’ metaphor
In the 19th century, biologists came to appreciate for the first time the fundamentality of the cell to all life on Earth. One of the early pioneers of cell biology, Rudolf Virchow, realized that the discovery of the cell brought with it a new way of seeing the organism. He described the organism as a ‘cell state’, or Zellenstaat, a ‘society of cells, a tiny, well-ordered state, with all of the accessories—high officials and underlings, servants and masters, the great and the small’ [1].
Virchow’s vision was widely supported in late 19th Century German biology. Ernst Haeckel, an influential early advocate of Darwinism, advocated the ‘cell state’ metaphor throughout his career, reflecting towards the end of it that:
‘The conception of cells as ‘elementary organisms’ led to the further opinion that our own human organism, just like all higher animals and plants, is actually a ‘cell state’, composed of millions of microscopic citizens, the individual cells, which work more or less independently, and co-operate for the common purpose of the entire state’ [2].
In Britain, meanwhile, the philosopher Herbert Spencer coined the notion of the ‘social organism’, a complex, two-way analogy between the cells of the body and the members of a society:
‘Hence we are warranted in considering the body as a commonwealth of monads, each of which has independent powers of life, growth, and reproduction; each of which unites with a number of others to perform some function needful for supporting itself and all the rest; and each of which absorbs its share of nutriment from the blood. And when thus regarded, the analogy between an individual being and a human society, in which each man, whilst helping to subserve some public want, absorbs a portion of the circulating stock of commodities brought to his door, is palpable enough’ [3].
In the 20th Century, the ‘cell state’ metaphor fell out of favour in biology. The rise of biochemistry and, later, molecular biology was accompanied by the emergence of a new metaphor: the notion of a cell as a factory, subordinate to the organism as a whole and dedicated to serving its biochemical needs [4]. Has the time now come for a revival of the ‘cell state’ perspective? Three trends in recent social evolution research suggest that it has.
Firstly, there is our growing awareness of the scale of cooperation among microorganisms (see Parts 1 and 3). Some social behaviours in microbes, such as the formation of a grex in social amoebas, result in phenomena that clearly resemble simple multicellular organisms. More controversially, some authors, such as Marc Ereshefsky and Makmiller Pedroso, have suggested that even biofilms should be regarded as multicellular individuals in their own right.
Secondly, in insect biology, there has been a revival of interest in the ‘superorganism’ concept: the suggestion that we should think of an insect colony as a single, higher-level organism. While this idea has always been controversial, even to consider it is to recognize the possibility that a high degree of social complexity can in principle give rise to a new, organism-like entity.
Thirdly, a research program called ‘major transitions theory’ has led to a radical re-evaluation of the place of cooperation in the history of life. Building on foundations laid by, among others, Leo Buss, John Tyler Bonner, and John Maynard Smith and Eörs Szathmáry, major transitions researchers portray the history of life as a series of ‘evolutionary transitions in individuality’ in which integrated, higher-level individuals have evolved, through social evolution, from groups of smaller entities.
When we look at evolution in this new light, we start to see social phenomena where we saw none before. We see cooperation among cells within multicellular organisms, among organelles within cells, even among genes within a chromosome. The result has been a dramatic increase in the explanatory ambitions of social evolution research—and the return of ‘cell state’ thinking.
Importantly, for social evolution theorists working on the origins of multicellular life, the ‘cell state’ is more than a metaphor: it’s the foundation for a research program. In other words, taking a ‘social perspective’ on the multicellular organism does not simply mean describing the activities of cells in social terms. It means drawing on the concepts and methods of social evolution theory to explain the evolutionary origins of multicellular individuals.
Hamilton’s hypothesis
For one of the pioneers of major transition theory, Leo Buss, the evolution of multicellular life presented the following puzzle: given that natural selection favours cells that promote their own reproduction, how did early multicellular organisms avoid being destabilized by conflict among cell lineages [5]?
His answer was that such organisms have evolved—through group selection—mechanisms for controlling internal conflict, such as ‘germline segregation’, whereby the capacity to generate a new organism is limited to a very small number of cell lineages (the germline) that are set aside early in development. This, however, led to a ‘chicken and egg’ puzzle: how could group selection be powerful enough, relative to individual selection, to assemble such mechanisms prior to the existence of such mechanisms?
However, when we view the organism through the lens of inclusive fitness, this puzzle dissolves. Multicellular organisms are clonal groups, and there is no reason for the cell lineages in a clonal group to be in evolutionary conflict. A clonal group is one in which the conditions are highly favourable to the evolution of altruism. As Hamilton himself observed:
‘Our theory predicts for clones a complete absence of any form of competition which is not to the overall advantage and also the highest degree of mutual altruism. This is borne out well enough by the behavior of clones which make up the bodies of multicellular organisms’ [6].
In other words, there is no big puzzle about the stability of cooperation among the cell lineages of the first multicellular organisms. These organisms were clonal groups, and they cooperated because they were genetically near-identical. No further mechanisms were needed to suppress competition, so no ‘chicken and egg’ problem arises. Let’s call this ‘Hamilton’s hypothesis’.
Queller has taken this hypothesis further, arguing that relatedness can even explain the origins of a ‘germ-soma’ division of labour. He suggests that ‘the germ line might have originated as a consequence of other cell lineages’ altruistically removing themselves from the reproductive line, to perform some somatic benefit to the organism’.
This turns the explanatory relationship posited by Buss on its head. Far from being a group-level adaptation for suppressing conflict among cells, the germline, on Queller’s account, arose as a by-product of altruism—altruism that evolved because the inclusive fitness interests of the cells were aligned.
Complications
Hamilton’s hypothesis is complicated by the fact that few organisms are fully clonal. Clonality is feature of organisms that develop from a single cell, but not all development is like this. For example, many plants can reproduce vegetatively, with the new individual developing from a multicellular offshoot.
In plants under cultivation, many generations of vegetative reproduction lead to the accumulation of mutations in different cell layers, resulting in individuals containing internal genetic diversity. In the wild, though, plants frequently reproduce sexually, pushing their lineage through a single-cell bottleneck and restoring high relatedness. Provided this happens often enough, high relatedness and low internal conflict will be maintained.
Even among organisms that pass through a single-cell bottleneck every generation, such as multicellular animals, clonality is not perfect. Within-organism genetic diversity can arise through ‘chimerism’, where cell lineages produced from a different sperm and egg mix in the early stages of development. We see this, for example, in marmosets.
Genetic diversity also arises through mutation. Sometimes, these mutation events lead to cancer, and the survival of the population depends on these cancerous ‘cheater’ lineages being unable to spread between organisms. We see a grim illustration of this point in the Tasmanian devil, now threatened with extinction due to an epidemic of facial tumours. Given this, we should not be surprised to find that an ability to discriminate ‘self’ from ‘non-self’, and to attack intruding cell lineages, is present even in sponges, often regarded as among the simplest multicellular animals.
Yet, for all these caveats, it remains plausible that, for any organism spawned from a single cell and of a size within certain bounds, relatedness is high enough to stabilize cooperation among the cells. It’s also plausible that organisms which can reproduce vegetatively in the wild pass through a single-cell bottleneck often enough to generate enough relatedness to stabilize cooperation among their cells. So Hamilton’s hypothesis has, I think, stood the test of time. The ultimate explanation for the stability of cooperation within multicellular organisms, at least up to a certain size, is genetic relatedness.
Open questions
So what still needs explaining about the origins of multicellular life, from the point of view of social evolution theory? Many of the most intriguing questions concern the process by means of which a social group of cells, once formed, is transformed over evolutionary time into a multicellular organism with a clear division of labour among distinct cell types. Andrew Bourke has called this process ‘social group transformation’ [7].
One open question here concerns the relationship between the size of a multicellular organism and its complexity. In the natural world, we find a clear positive correlation between the total number of cells an organism contains and the number of distinct, specialized cell types it contains. What explains this relationship?
Another concerns the limits on the number of cell types. There may have been as many as 25 separate instances of the evolution of multicellular life, but in only three of these cases—the plants, animals, and fungi—has the lineage in question proceeded to evolve large numbers of distinct cell types. It seems that evolving high numbers of specialized cell types remains improbable even once a lineage has attained evolved multicellularity. Indeed, it suggests that special further conditions are required. What are these conditions?
For now, I will simply leave these questions open. Some possible answers are developed in Chapter 7 of The Philosophy of Social Evolution.
[1] R. Virchow, 1859, ‘Atoms and Individuals’, in L. J. Rather, ed., Disease, Life, and Man: Selected Essays by Rudolf Virchow, Stanford University Press, p. 124.
[2] Quoted in A. Reynolds, 2008, ‘Ernst Haeckel and the Theory of the Cell State: Remarks on the History of a Bio-Political Metaphor’, History of Science, 6, p. 128.
[3] H. Spencer, 1851, Social Statics, 1st ed., John Chapman, p. 451.
[4] Reynolds, op. cit.
[5] L. Buss, 1987, The Evolution of Individuality, Princeton University Press.
[6] W. D. Hamilton, 1964, ‘The Genetical Evolution of Social Behaviour’ I and II, Journal of Theoretical Biology, 7, p. 25.
[7] A. F. G. Bourke, 2011, Principles of Social Evolution, Oxford University Press.
This post was originally published on The Brains Blog, 2 November 2017
Part 5. Cultural inclusive fitness?
The Cuevas de Las Manos, Argentina. Image: Mariano
The scale of human cooperation
If you start with the assumption that biological altruism evolves because the benefits fall on genetic relatives, the scale of human social organization is puzzling. We cooperate with huge numbers of individuals who are not genetic kin—large-scale modern societies depend on it.
Not all of this cooperation is altruistic—a lot of it is mutually beneficial. We do it for the immediate returns, or to avoid punishment, or for long-term returns mediated by reciprocity and reputation. But all of this mutually beneficial cooperation rests on a basic platform that must have evolved at a relatively early stage in human social evolution, and that calls for explanation in its own right: namely, a tendency to interact peacefully by default with strangers.
To see what I mean, consider what happens when a chimpanzee strays into the territory of a rival group. Given the chance, a patrol from the home group will attack and kill the intruder without a moment’s hesitation. This is why chimps do not have tribes. Their territorial aggression towards outsiders restricts them to small residential groups of 15 to 150 individuals. These groups never aggregate to form the much larger, ‘tribal’ units of thousands of individuals characteristic of human social organization in stateless societies.
Something happened in human evolution to change this situation. Individuals, rather than acting aggressively by default towards members of neighbouring residential groups (or ‘bands’), came to interact peacefully with them. Larger, tribal units composed of many bands became possible—units that often waged war on each other, but in an organized way that involved a remarkable level of intra-tribal cooperation among large numbers of genetic non-relatives. In one of the most important transitions in human evolution, the pacification of inter-group relations at small scales brought a new level of organization—the ‘tribal’ level—into existence.
This non-violence towards members of neighbouring groups began, I suspect, as a form of biological altruism. In a population in which the default is to kill outsiders, to spare one confers an obvious benefit on the recipient. But there is also a cost to the actor, in the form of a risk that the spared individual will injure or kill you or one of your relatives, or make off with food or other resources. This is a risk that chimps are not willing to take.
From genes to culture
We don’t know why this form of altruism first evolved. Genetic relatedness may have had some role: when there is significant interbreeding between groups, individuals in different bands may still be genetic relatives to some degree, even if they are strangers to each other [1]. But I doubt whether genetic relatedness would have been high enough. Studies of present-day hunter-gatherers by Kim Hill and colleagues suggest that, because there is so much migration between bands, genetic relatedness is actually very low indeed.
A different possibility is that human prosocial dispositions are products of cultural evolution. In recent years, many theories and models of cultural evolution—that is, the evolution of beliefs, values, skills, and other ‘cultural variants’—have been developed. The field is thriving, and the concept of ‘cultural group selection’ in particular is gaining traction. But concepts of inclusive fitness and relatedness, despite being incredibly valuable for understanding genetic social evolution, are notable by their absence.
In Chapter 8 of The Philosophy of Social Evolution, I consider the prospects for a theory of cultural inclusive fitness, and I ask whether might it be able to provide a better account of the origin of large-scale human cooperation than the traditional genetic version.
Cultural inclusive fitness: the basic idea
Just as the basic idea of inclusive fitness is easiest to understand by adopting a gene’s eye perspective (without it thereby being equivalent to this perspective), the basic idea of cultural inclusive fitness is easiest to understand by positing memes in Richard Dawkins’s sense—discrete, gene-like units of cultural inheritance—and adopting a ‘meme’s eye view’ on cultural evolution.
Suppose, then, that you are a meme in a population in which cultural transmission is exclusively parental and entirely unbiased—that is, people only ever acquire memes from their biological parents, and they get a random sample of their parents’ memes. These are not realistic assumptions (see below), but they make the analogy with genetic inheritance as close as possible.
Like a gene, you have two ways to achieve your goal of increasing your representation in future generations. One is to promote the reproductive success of your host. The other is to increase the number of offspring of others who are more likely than average to possess copies of you. In the right circumstances, it may be in your interests to help others at a cost to your own bearer, if the total number of copies you leave in future populations is thereby increased.
This case is exactly analogous to a traditional case of kin selection. Note, though, that the likelihood of two individuals sharing a particular meme may differ from their likelihood of sharing a particular gene. Cultural inheritance, even when exclusively parental, is still a different process from genetic inheritance, and it may lead to different correlations between relatives. In principle, cultural relatedness could be high even though genetic relatedness is low, or vice versa.
In this process, the condition for the spread of a cultural variant is given by a cultural analogue of Hamilton’s rule. It’s a rule with the same ‘rb > c’ form, but now r is cultural relatedness rather than genetic relatedness—it’s a formal measure of the cultural similarity, not genetic similarity, between social partners.
Blending inheritance
Although the rationale for the cultural analogue of Hamilton’s rule is easiest to see by looking at cultural evolution from the perspective of an imaginary meme, the mathematical result does not rely on a meme-like conception of cultural inheritance. The result still holds even if beliefs, skills, values, etc. are modelled as quantitative traits that are not at all meme-like, but rather blend together—in other words, the result still holds if your children inherit a messy blend of your beliefs, skills, values, etc. rather than a high-fidelity copy.
In short, memes are a ladder we can kick away. A more general notion of cultural relatedness—a measure of the statistical association between the quantitative ‘cultural variants’ of interacting agents—is a more useful concept that does not assume particulate cultural inheritance. This is the key advantage of cultural inclusive fitness over memetics—it requires no assumption of particulate inheritance, and aims to derive results that still hold on the assumption of blending inheritance.
Humans and microbes
Obviously, our original assumption that cultural transmission is exclusively parental and entirely unbiased—an assumption we made to get the closest possible analogy with genetic kin selection—is an unrealistic assumption. Cultural transmission is not exclusively parental: people acquire beliefs and values from others who are not their biological parents. And it is far from unbiased: some cultural traits are much more likely to be transmitted than others.
Crucially, though, the tools we develop to accommodate these complications in the case of microbial evolution (see Part 3) can also be usefully applied to the human case. Humans have rediscovered something that is widespread in bacteria, but that went missing for a few hundred million years of animal evolution—we have rediscovered horizontal transmission. Ways of incorporating horizontal transmission into models of microbial evolution also help us incorporate it into models of human evolution.
The upshot is that I think the prospects are good for a theory of cultural inclusive fitness, based on something like the diachronic concept of relatedness I developed for use in the case of bacterial evolution (see Part 3). In Chapter 8 of The Philosophy of Social Evolution, I take some initial steps towards developing such a theory. But the theory is at an early stage and there is much left to do.
Cultural inclusive fitness in human evolution
Let’s now return to the puzzle I introduced earlier. How did the scope of human altruism come to extend beyond the limits of the immediate residential camp or band, to encompass an extended ‘tribal’ social network of hundreds, and eventually thousands, of individuals?
The currently popular theory of cultural group selection seems to struggle with this puzzle: the large ‘tribal’ groups presupposed by cultural group selection models do not yet exist (how they come to exist is what needs explaining), and group selection at the level of the band will not select for cooperation between members of distinct bands.
Cultural inclusive fitness, however, may be of use. Patterns of migration between bands create extended networks of acquaintance, friendship and kin relations—each individual has a large network centred on itself, consisting not just of immediate friends and kin, but of friends of friends and kin of kin. Many of the ‘strangers’ in neighbouring groups will be friends of friends or kin of kin. If present-day chimpanzees are any guide, the common ancestor of humans and chimps would have treated all members of other bands with hostility. However, a process of ‘cultural kin selection’ might favour a reduction of inter-band aggression.
Why? Because strangers from adjoining bands would have been culturally related. A study of present-day hunter-gatherer social networks by Coren Apicella and colleagues shows that cultural variants, including tendencies towards prosocial behaviour, are correlated across two degrees of separation. Your friends’ friends, who may be unfamiliar to you, live far away from you and be genetically unrelated to you, will nevertheless tend to have beliefs and values that are correlated with yours.
This is probably due to a mix of conformist bias (people tend to conform to the average beliefs and values of their social network) and assortative network formation (people tend to interact more often with people culturally similar to themselves). Whatever the cause, the result is that, when you meet strangers from neighbouring camps, they are probably your cultural relatives, and it may increase your cultural inclusive fitness to help them, or least to refrain from hurting them.
This can lead to the selection of prosocial beliefs and values under a process of cultural selection. In such a process, prosocial beliefs, such as the belief that one should not harm members of a neighbouring camp, spread for fundamentally the same reason genes for altruism spread—because the benefits they generate fall differentially on other bearers of the same belief.
This is a hypothesis about how multi-band, ‘tribal’ social groupings originally got started. It is a speculative and unconfirmed hypothesis. It relies on cultural correlations existing in extended social networks between individuals who are more or less strangers to each other—and there is evidence of this. But the evidence is far from sufficient to call the hypothesis confirmed.
Still, it is enough to show that there is serious work for a theory of cultural inclusive fitness to do. We don’t know how large-scale social organization began in the human lineage. We don’t know how the scope of human altruism and prosociality came to extend so far beyond the network of one’s genetic kin—bucking the trend in the rest of the natural world. The concept of cultural inclusive fitness may help us develop a solution to that puzzle.
[1] This possibility is explored by Bernard Chapais in his book Primeval Kinship (2008, Harvard University Press).
This post was originally published on The Brains Blog, 3 November 2017